Answer:
The table represents a linear function.
The graph of linear function y = 3x is attached below.
Explanation:
Given the table
Number of Hours 1 3 5
Number of Tents 3 9 15
Given that the slope is 3.
Finding the slope between (1, 3) and (3, 9)
Slope = (y₂-y₁) / (x₂-x₁)
= [9-3] / [3-1]
= 6 / 2
= 3
Finding the slope between (3, 9) and (5, 15)
Slope = (y₂-y₁) / (x₂-x₁)
= [15-9] / [5-3]
= 6 / 2
= 3
As the value of slope remains constant i.e. slope = m = 3.
Using the point-slope form of the line equation
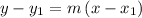
where m is the slope of the line and (x₁, y₁) is the point
substituting the values m = 3 and the point (1, 3)
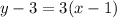
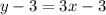

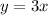
Comparing with the slope-intercept form of a linear function of line
y = mx+b where m is the slope and b is the y-intercept
slope = 3 and y-intercept b = 0
Therefore, the table represents a linear function.
The graph of linear function y = 3x is attached below.