Question

Write three consecutive numbers starting with number n+1, where n is natural number. Find the sum of those numbers and prove that it is divisible by 3.

Answer 1

Consecutive numbers differ by one, which means that if you start with a certain integer
`x`, you obtain the next integer by adding one.

So, if you start with
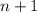`n+1`, the three consecutive numbers are

`n+1,\quad (n+1)+1 = n+2,\quad (n+2)+1 = n+3`

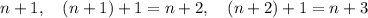
The sum of these three numbers is

`(n+1) + (n+2) + (n+3) = 3n+6`

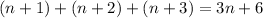
This number is divisible by 3 because you can write it as

`3n+6 = 3(n+2)`

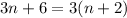
Note that this is true in general: the sum of three consecutive numbers is always divisible by three, because it is three times the middle number.