Answer:
It shrinks the graph vertically to 1/4 its original height ⇒ 1st answer
Explanation:
* Lets revise the vertical stretch and shrink
- A vertical stretching is the stretching of the graph away from the
x-axis
- If k > 1, the graph of y = k • f(x) is the graph of f(x) vertically
stretched by multiplying each of its y-coordinates by k
- A vertical shrink is the squeezing of the graph toward
the x-axis.
- If 0 < k < 1 (a fraction), the graph of y = k • f(x) is the graph of f(x)
vertically shrank by multiplying each of its y-coordinates by k
* Now lets solve the problem
∵ The function

∵ The parent function is y = x²
- The parent function y = x² is multiplied by a factor
∴ The parent function is stretched or shrank vertically
∵ The factor is

∵
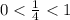
∴ The parent function shrinks vertically by scale factor

∵ When the graph shrank vertically, then each y-coordinates oo the
point lie on the graph multiplied by 1/4
- That means the height of the graph is 1/4 of the height of the original
∴ The answer is the graph shrank vertically to 1/4 its original height
* It shrinks the graph vertically to 1/4 its original height