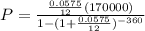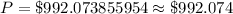Answer:
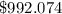
Explanation:
Since, the periodic payment of a loan,
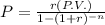
Where, P.V. is the principal amount,
r is the rate per period,
n is the number of periods,
Given,
P.V. = $ 170,000,
Annual rate = 5.75 % = 0.0575,
Thus, the rate per month,

Also, time = 30 years,
So, the number of months in 30 years,
n = 360 ( 1 year =12 months )
Hence, the monthly payment of the loan is,