Given:
The graph of a line.
To find:
The equation of line and values of m and b. Check whether it is proportional or linear.
Solution:
From the given graph it is clear that, the line passes through (0,4) and (2,0). So, the equation of line is
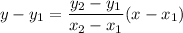
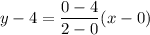
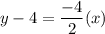
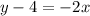
Adding 4 on both sides, we get
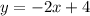
On comparing this equation with slope intercept form, i.e.,
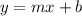 , we get
, we get
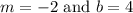
All lines are linear. If a line passes through the origin then it is proportional.
From the given graph it is clear that the line is not passing through the origin, i.e., (0,0). So, it is linear not proportional.
Therefore, the value of m is -2 and the value of b is 4. The equation of line is
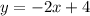 . The line linear not proportional because it does not passing through the origin.
. The line linear not proportional because it does not passing through the origin.