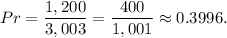Question

A jar of alphabet tiles contains 10 unique consonant tiles an 5 unique vowel tiles. If 5 tiles are picked randomly, the probability that 3 are consonants and 2 are vowels is

Answer 1

400/1001

Explanation:

For PLATO mastery test!

Answer 2

`(400)/(1,001)\approx 0.3996`

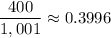
Explanation:

There are 10 unique consonant tiles an 5 unique vowel tiles, 15 tiles in total.

You can select 5 different tiles in

`C^(15)_5=(15!)/(5!(15-5)!)=(11\cdot 12\cdot 13\cdot 14\cdot 15)/(2\cdot 3\cdot 4\cdot 5)=11\cdot 13\cdot 7\cdot 3=3,003`

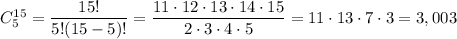
different ways.

You can select 3 different consonants and 2 different vowels in

`C^(10)_3\cdot C^5_2=(10!)/(3!(10-3)!)\cdot (5!)/(2!(5-2)!)=(8\cdot 9\cdot 10)/(2\cdot 3)\cdot (4\cdot 5)/(2)=4\cdot 3\cdot 10\cdot 2\cdot 5=1,200`

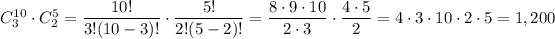
different ways.

Thus, the probability is

`Pr=(1,200)/(3,003)=(400)/(1,001)\approx 0.3996.`