Question

Identify an equation in point-slope form for the line perpendicular to

y=1/4x-7 that passes through (-2,-6).
A. y+6= -4(x+2)
B. y+6= -1/4(x+2)
C. y+2 = -4(x+ 6)
D. y-6=1/4(x-2)

Answer 1

Given:

Equation of line is
`y=(1)/(4)x-7`.

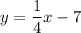The perpendicular line passes through (-2,-6).

To find:

The point slope form of perpendicular line.

Solution:

We have,

`y=(1)/(4)x-7`

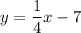
On comparing this equation with
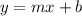`y=mx+b`, we get

`m=(1)/(4)`

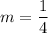
Slope of given line is
`(1)/(4)`.

Product of slopes of two perpendicular of the lines is -1.

So,
`Slope* (1)/(4)=-1`

`Slope=-4`

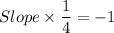
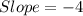
Slope of required line is -4 and it passes through (-2,-6). So, the point slope form is

`y-y_1=m(x-x_1)`

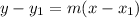
where, m is slope.

`y-(-6)=-4(x-(-2))`

`y+6=-4(x+2)`

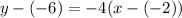
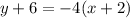
Therefore, the correct option is A.