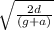Please help!
A pulley system is hanged in a lift as shown below in the
figure. A and B are two masses each having m and 2m mass
respectively. If d is the distance from the floor to B and the
lift starts to move with acceleration a, the time taken by B to reach the floor is,
1)
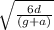
2)
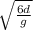
3)
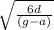
4)
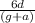
5)