Answer:
The work done by picking up 100 20-L bottles and raising it vertically 1 meter is 19614 joules.
Step-by-step explanation:
By the Work-Energy Theorem, the work needed to raise vertically 100 bottles of water is equal to the gravitational potential energy, units for work and energy are in joules:
 (1)
(1)
Where:
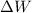 - Work.
- Work.
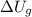 - Gravitational potential energy.
- Gravitational potential energy.
The work is equal to the following formula:
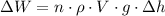 (2)
(2)
Where:
 - Number of bottles, dimensionless.
- Number of bottles, dimensionless.
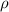 - Density of water, measured in kilograms per cubic meter.
- Density of water, measured in kilograms per cubic meter.
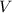 - Volume, measured in cubic meters.
- Volume, measured in cubic meters.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
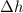 - Vertical displacement, measured in meters.
- Vertical displacement, measured in meters.
If we know that
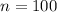 ,
,
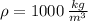 ,
,
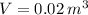 ,
,
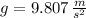 and
and
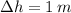 , then the work done is:
, then the work done is:
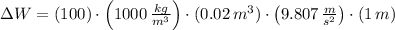
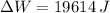
The work done by picking up 100 20-L bottles and raising it vertically 1 meter is 19614 joules.