Answer:
14.15ft
Explanation:
Attached is a visual representation of our scenario.
The green line represents the line of sight of the bird, and the green angle represents the angle of depression. It goes downwards because it says "depression."
As you can observe, the scenario creates a right triangle, where the alternate interior of the angle is found in the triangle.
Using Trigonometric Functions, or SOHCAHTOA, we can solve for the distance between the bird and the food, which in this case is the hypotenuse(H) of the triangle. Looking at the diagram again, we can see that 11ft was also given, which can be represented as the adjacent (A) side of the triangle. It is adjacent because it is right next to the angle given.
Because we have an angle and the adjacent side, we will use CAH.
Given:
A= 11ft
H = x
θ = 39°
Solution:
CAH
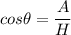
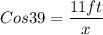
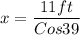
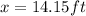
The bird is 14.15 ft away from the food.