Question

The local museum had 20000 visitors in 1990 . The number of visitors has decreased by 3% each year since 1990 . Enter a function m(x) to represent the number of visitors to the museum x years after 1990

Answer 1

It is m(x) = 20,000(0.97)^x.

Explanation:

After 1990, each year has (100-3) = 97% ( or 0.97) of visitors that it had the previous year.

So m(x) = 20,000(0.97)^x (answer).

Answer 2

`m(x)=20,000\cdot (0.97)^x`

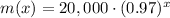
Explanation:

We have been that the local museum had 20000 visitors in 1990 . The number of visitors has decreased by 3% each year since 1990.

We will use exponential function to write formula for the given problem as number of visitors decrease exponentially.

We know that an exponential function is in form
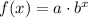`f(x)=a\cdot b^x`, where,

a = Initial value,

b = For decay b is in form (1-r), where r represents rate in decimal form.

Let us convert our given rate in decimal form.

`3\%=(3)/(100)=0.03`

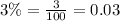
Upon substituting our given values in above formula we will get,

`m(x)=20,000\cdot (1-0.03)^x`

`m(x)=20,000\cdot (0.97)^x`

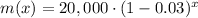
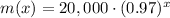
Therefore, the function
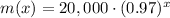`m(x)=20,000\cdot (0.97)^x` represents the number of visitors to the museum x years after 1990.