For this case, we must find an expression equivalent to:
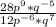
By definition of power properties we have:
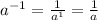
Rewriting the previous expression we have:
We take into account that:
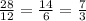
So:
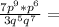
According to one of the properties of powers of the same base, we must put the same base and add the exponents:
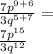
Answer:
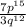
Option B