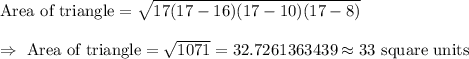Question

What is the area of triangle ABC ? round to the nearest square unit ?

Answer 1

33 square units

Explanation:

got it right

Answer 2

Answer: 33 square units

Explanation:

Given: Sides lengths of the triangle : 16 units, 10 units, 8 units.

Heron's formula:-

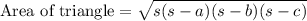`\text{Area of triangle}=√(s(s-a)(s-b)(s-c))`, where s is the semiperter and a,b and c are the side-lengths of the triangle.

Let a=16 , b=10 and c=8

Then,

`s=(a+b+c)/(2)=(16+10+8)/(2)=17`

Using Heron's formula:-

`\text{Area of triangle}=√(17(17-16)(17-10)(17-8))\\\\\Rightarrow\ \text{Area of triangle}=√(1071)=32.7261363439\approx33\text{ square units}`