Question

Elevation and depression in mathematics. Questions in images. Thanks!

Answer 1

QUESTION 1

Let us determine the value of
`x` first.

Using the tangent ratio;

`\tan(22\degree)=(x)/(60)`

`\Rightarrow x=60\tan(22\degree)`

`\Rightarrow x=24.2ft`

The height of the barn from the ground is
`5+24.2=29.2ft` to the nearest tenth.

QUESTION 2

We use the alternate interior angle property to obtain one of acute angles of the triangle to be
`4\degree`. See diagram.

We now use the sine ratio to get;

`\sin(4\degree)=(3208)/(x)`

This implies that;

`x=(3208)/(\sin(4\degree))`

We simplify to get;

`x=45988.56`

The airplane is about 45988.6 feet away.

Answer 2

1) 29.2 feet ( approx)

2) 45988.6 feet.

Explanation:

1) By the given diagram,

We can write,

`tan 22^(\circ) = (x)/(60)`

`\implies x = 60* tan22^(\circ) = 24.2415735501\approx 24.2`

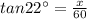
Thus, the height of the barn from the ground = 24.2 + 5 = 29.2 feet ( Approx)

2) By the Alternative interior angle theorem,

The angle of elevation in this situation ( shown in the below diagram ) must be same as angle of depression and equals to 4°,

Hence, we can write,

`sin4^(\circ)=(3208)/(x)`

`x = (3208)/(sin4^(\circ))=45988.5631801\approx 45988.6`

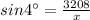
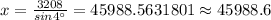
Thus, the plane is approximately 45988.6 feet away.