Question

The length of a rectangle is eight more than twice its width. The perimeter is 96 feet. Find the dimensions of the rectangle

Answer 1

The width of the rectangle is 14'8", and the length is 33'4"

Explanation:

We're given two pieces of information:

The length is eight more than twice the width:

`l = 2w + 4`

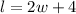
The perimeter is 96 feet:

`p = 96`

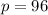
We also need to apply one more piece of information that is not provided here, and that is the relationship between the perimeter of a rectangle, and it's length and width:

`p = 2l + 2w`

We can solve for w by plugging the other two values into the last:

`p = 2w + 2l\\96 = 2w + 2(2w + 4)\\96 = 2w + 4w + 8\\88 = 6w\\3w = 44\\w = (44)/(3)\\w = 14(2)/(3)`

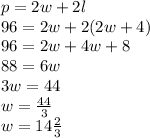
Now we can find the length by plugging w into the first equation:

`l = 2w + 4\\l = 2(14(2)/(3)) + 4\\l = 29(1)/(3) + 4\\l = 33(1)/(3)`

One third of a foot is four inches, so the width is 14'8" and the length is 33'4"

To make sure our answer is correct, we should plug those numbers back into the area equation and see if we're right:

`p = 2l + 2w\\p = 2(33(1)/(3)) + 2(14(2)/(3))\\p = 66(2)/(3) + 29(1)/(3)\\p = 96`

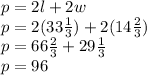
So we know our answer's correct