Question

Use the following pair of points to find the slope, midpoint, distance between the points and the equation of the line containing the two points. Use (2, 4) and (-3, 9)

Answer 1

Answer to Q1:

Slope = m = -1

Explanation:

We have given two points.

Let (x₁,y₁) = (2, 4) and (x₂,y₂) = (-3, 9)

We have to find the slope of the equation of the line containing the two points.

Slope is defined as the steepness of the line.

The formula to find slope of the line is:

Slope = m =
`(y_(2)-y_(1)  )/(x_(2)-x_(1)  )`

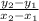
Putting given values in above formula, we have

Slope = m =
`(9-4)/(-3-2)`

Slope = m =
`(5)/(-5)`

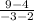
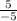
Slope = m = -1 which is the answer.

Answer to Q2:

`((-1)/(2),(13)/(2))`

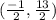
Explanation:

We have given two points.

Let (x₁,y₁) = (2, 4) and (x₂,y₂) = (-3, 9)

We have to find the Mid-point of the line segments whose end-points are given.

Mid-point is halfway between two end-points of the line segment.

The formula to find Mid-point is:

M =
`((x_(1) +x_(2) )/(2),(y_(1)+y_(2)  )/(2))`

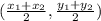
Putting given values in above formula , we have

M =
`(2-3)/(2) ,(4+9)/(2)`

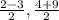
M =
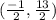`((-1)/(2),(13)/(2))` Which is the answer.

Answer to Q3:

d = 5√2 units

Explanation:

We have given two points.

Let (x₁,y₁) = (2, 4) and (x₂,y₂) = (-3, 9)

We have to find the distance between two points.

The formula to find the distance between two points is:

d = √(x₂-x₁)²+(y₂-y₁)²

Putting values in above formula, we have

d = √(-3-2)²+(9-4)²

d = √(-5)²+(5)²

d = √25+25

d = √50 = √25×2

d = 5√2 units

Hence, distance between the two given points is √50 units.

Answer to Q4:

y = -x+6

Explanation:

We have given two points.

(2, 4) and (-3, 9)

We have to find the equation of the line.

y = mx+c is equation of line where m is slope and c is y-intercept.

We have already find the slope of the equation of line.

m = -1

Now , we have to find the y-intercept of the equation.

Putting the value of slope and one point in equation of ine, we have

4 = (-1)(2)+c

4 = -2+c

c = 4+2

c = 6

hence, equation of line is y = (-1)x+(6)

y = -x+6 which is the answer.

Answer 2

QUESTION 1

Let
`(x_1,y_1)=(2,4)` and
`(x_2,y_2)=(-3,9)`.

The slope is given by the formula;

`m=(y_2-y_1)/(x_2-x_1)`

We substitute the values into the formula to get;

`m=(9-4)/(-3-2)`

Simplify;

`m=(5)/(-5)`

The slope is;

`m=-1`

QUESTION 2

Let
`(x_1,y_1)=(2,4)` and
`(x_2,y_2)=(-3,9)`.

The midpoint is given by the formula;

`M=(((x_1+x_2)/(2),(y_1+y_2)/(2))`

Put these values into the formula to get;

`M=(((2+-3)/(2),(4+9)/(2))`

The midpoint is

`M=(((-1)/(2),(13)/(2))`

QUESTION 3

Let
`(x_1,y_1)=(2,4)` and
`(x_2,y_2)=(-3,9)`.

The distance between the two points can be calculated using the formula;

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`.

We substitute the values to obtain;

`d=√((-3-2)^2+(9-4)^2)`.

Simplify;

`d=√((-5)^2+(5)^2)`

`d=√(25+25)`

`d=√(50)`

The distance is
`d=5√(2)`.

QUESTION 4

Let
`(x_1,y_1)=(2,4)` and
`(x_2,y_2)=(-3,9)`.

The equation can be found using the point-slope formula given by;

`y-y_1=m(x-x_1)`, where
`m=-1` is the slope.

We plug in the values to get;

`y-4=-1(x-2)`

We expand the bracket to get;

`y-4=-x+2`

`y+x=2+4`

The equation of the line is;

`y+x=6`