Answer:
a)False
b)False
c)True
d)False
Explanation:
a. False
Let us first compute the minutes-per-mile of each:
Carrie: 10mi in 85 mins
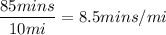
So for every mile it takes Carrie 8.5 minutes
Allison: 15mi in 135mins
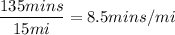
So for every mile it takes Allison 9 minutes
As you can see, it Allison pace was slower because it takes her a longer time to complete 1 mile.
b. False
Let us compute this time miles per hour, before we do that though, you need to remember that the units are in minutes, so we need to convert them into hours (1 hour = 60 minutes):
Carrie: 10 miles in 85 minutes
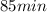 x
x
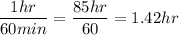
We use that to get our miles per hour (mph):
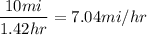
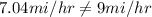
As you can see Carrie's rate is actually 7.04 mi/hr and NOT 9 mi/hr.
c. True
Allison: 15 miles in 135 mins
The question is whether:
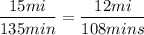
To determine if two fractions are proportional, all you need to do is cross multiply and see if the products are equal:

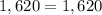
Because they are equal, then it is TRUE.
We can also solve it by solving the rate of each.
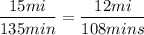
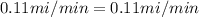
d. False
To solve this, just take the minutes per mile of each to see how long each took to reach 9 miles. You can do this by multiplying the minutes per mile of each and multiplying it to 9 miles.
Carrie: 8.5 min/mi
Allison: 9 min/mi
With that alone you can already deduce that Carrie is not SLOWER. But if you need to show the solution, we can move on. We multiply both rates by 9 miles, so we can see how long it took each.
Carrie:
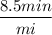 x
x
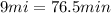
Allison:
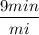 x
x
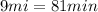
The question is whether if Carrie is slower than Allison, so you find the difference (subtract). And there you can see, that the difference is 4.5 mins.
However, since Carrie has the lower value, it means that she was actually faster.