Question

Find the limit, if it exists.
Picture provided below.

Answer 1

c. 20

General Formulas and Concepts:

Calculus

Limits

Limit Rule [Constant]:
`\displaystyle \lim_(x \to c) b = b`

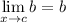
Limit Rule [Variable Direct Substitution]:
`\displaystyle \lim_(x \to c) x = c`

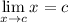
Limit Property [Addition/Subtraction]:
`\displaystyle \lim_(x \to c) [f(x) \pm g(x)] = \lim_(x \to c) f(x) \pm \lim_(x \to c) g(x)`

Limit Property [Multiplied Constant]:
`\displaystyle \lim_(x \to c) bf(x) = b \lim_(x \to c) f(x)`

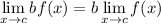
Explanation:

We are given the following limit:

`\displaystyle \lim_(x \to 2) (3x^3 + x^2 - 8)`

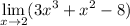
Rewriting this limit using limit properties, we obtain:

`\displaystyle \lim_(x \to 2) (3x^3 + x^2 - 8) = 3\lim_(x \to 2) x^3 + \lim_(x \to 2) x^2 - \lim_(x \to 2) 8`

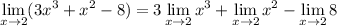
Evaluate the limits using various limit rules:

`\displaystyle \lim_(x \to 2) (3x^3 + x^2 - 8) = 3(2)^3 + (2)^2 - 8`

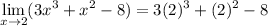
Simplify:

`\displaystyle \lim_(x \to 2) (3x^3 + x^2 - 8) = 20`

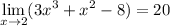
And we have our answer.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits