Answer:
A.
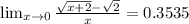
Explanation:
We are given the limit expression,

As, we see that,
When
 , the function is of the form
, the function is of the form
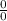 .
.
So, we will use L'Hospital's Rule to proceed further i.e. Differentiate the numerator and denominator with respect to x.
That is,

implies
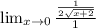
i.e.
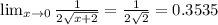
Thus,
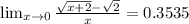
Hence, option A is correct.