Question

Estimate the limit.
Picture provided below.

Answer 1

Explanation:

Answer 2

Choice d is correct.

Explanation:

We have the given function :

`\lim_(x \to \6) x-3/x^(2) -9`

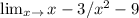
We have to find the limit.

First, simplify the denominator of function.

x²-9 = (x-3)(x+3)

Put this simplification in the function we get,

`\lim_(x \to \6) x-3/(x-3)(x+3)`

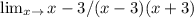
finally we simplify the function we get,

`\lim_(x \to \6) 1/x+3`

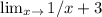
Apply the limit to the function we get,

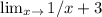`\lim_(x \to \6) 1/x+3` = 1/9 = 0.1111111

Choice d is correct.