Answer:
Shown below
Explanation:
First of all, we need to plot the equation:
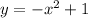
The graph of this equation is a parabola. The vertex of this parabola lies on the point (0, 1) and the x-intecepts are the points (-1, 0) and (1, 0). But the problem asks for the graph of y greater than or equal to -x^2 + 1, that is, the inequality:

To find this, we choose a point on the Cartesian plane, say, (0, 0) and let's take a look to the inequality:
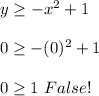
So the region does't contain point (0, 0), therefore the graph is the one shown below.