Question

Use the definition of continuity and the properties of limits to show that the function h(x)=x+3/(x2-x-1)(x2+1) is continuous at x = -2.

Picture provided below.

Answer 1

We are asked to use the property of limit and continuity to show that the function h(x) is continuous at x= -2.

The function h(x) is given by:

`h(x)=(x+3)/((x^2-x-1)(x^2+1))`

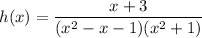
since clearly as we know that Polynomial functions are continuous everywhere so, the term in the numerator is continuous at x= -2.

Also the term in the denominator is continuous at x= -2.

and the function h(x) is defined in the neighbourhood of x= -2 since the denominator is not equal to zero at x= -2.

Also at x= -2 ; the limit of the function h(x) exist .

The limit is given by:

`h(x)= \lim_(x \to -2) (x-2)/((x^2-x-1)(x^2+1))\\\\h(x)=(-2-2)/((-2)^2-(-2)-1)((-2)^2+1))\\\\h(x)=(-4)/(4+2-1)(4+1))\\\\h(x)=(-4)/(5* 5)\\\\h(x)=(-4)/(25)`

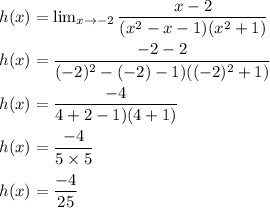
Hence, the function is continuous at x= -2.