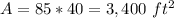Question

Mr. Crow, the head groundskeeper at High Tech Middle School, mows the lawn along the side of the gym. The lawn is rectangular, and the length is 5 feet more than twice the width. The perimeter of the lawn is 250 feet.

a. find the dimensions of the lawn.

b. Use the dimensions you calculated in part (a) to find the area of the lawn.

Answer 1

Part A) The dimensions of the lawn are

`L=85\ ft`,
`W=40\ ft`

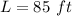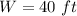
Part B) The area of the lawn is
`3,400\ ft^(2)`

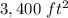
Explanation:

Let

L------> the length of the rectangular lawn

W----> the width of the rectangular lawn

Part A) Find the dimensions of the lawn

we know that

The perimeter of a rectangle is equal to

`P=2(L+W)`

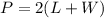
we have

`P=250\ ft`

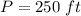
so

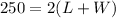`250=2(L+W)` -------> equation A

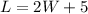`L=2W+5` -----> equation B

substitute equation B in equation A

`250=2(2W+5+W)`

`250=4W+10+2W`

`6W=250-10`

`W=40\ ft`

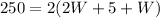
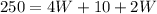
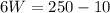
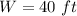
find the value of L

`L=2W+5` ----->
`L=2(40)+5=85\ ft`

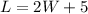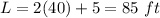
Part B) Use the dimensions you calculated in part (a) to find the area of the lawn

we know that

The area of a rectangle is equal to

`A=LW`

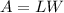
we have

`L=85\ ft`,
`W=40\ ft`

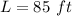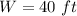
substitute in the formula

`A=85*40=3,400\ ft^(2)`