Answer:
Option c is answer
Explanation:
A function is given as
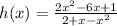
Limit is to be found out for x tends to infinity.
We find that numerator and denominator has the same degree.
HEnce a horizontal asymptote exists
COefficients of leading terms are 2 and -1 respectively
Asymtote would be y =2/-1 = -2
Alternate method:
When x tends to infinity, 1/x tends to 0
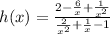
by dividing both numerator and denominator by square of x.
Now take limit as 1/x tends to 0
we get
limit is y tends to 2/-1 =-2
Hence horizontal asymptote is y =-2