Question

Help Please...................

Answer 1

(a, b, c, d) = (0, 1, 1, 3)

Explanation:

`(4xy^3+8x^2y^5)/(2xy^2)=(4xy^3)/(2xy^2)+(8x^2y^5)/(2xy^2)\\\\=(4)/(2)x^(1-1)y^(3-2)+(8)/(2)x^(2-1)y^(5-2)=2x^0y^1+4x^1y^3`

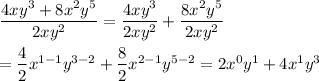
The exponents of interest are ...

• a = 0
• b = 1
• c = 1
• d = 3

_____

The applicable rule of exponents is ...

(a^b)/(a^c) = a^(b-c)

This is easy enough to remember if you remember that an exponent signifies repeated multiplication. Factors common to numerator and denominator cancel, so the remaining number of factors is the difference between the number in the numerator and the number in the denominator.

y^5/y^2 = (y·y·y·y·y)/(y·y) = y·y·y = y^(5-2) = y^3

Answer 2

2 *x^0 *y^1 +4 x^1 y^3

Explanation:

4xy^3 + 8x^2y^5

----------------------------

2xy^2

Divide this into 2 fractions

4xy^3 8x^2y^5

---------- + ------------------

2xy^2 2xy^2

Remember when dividing exponents a^b/ a^c = a^(b-c)

4/2 x^(1-1) y^(3-2) + 8/2 x^(2-1) y^(5-2)

2 *x^0 *y^1 +4 x^1 y^3