Question

Leaves were falling off a tree at an exponential rate beginning Oct.1, on the 10th there were 5287 leaves. On the 21st there were 692 leaves

Y=Ae^kt

a) Find K (constant of proportionality)

B) how many leaves were there on the tree before it started losing leaves?

C) on what date was there only one leaf?

Any insight is appreciated

Answer 1

lemme use a slightly different equation, just the variables differ, but is basically the same you have there.

A)

`\bf \textit{Amount of Population Growth, \boxed{\textit{10th day}}} \\\\ A=Pe^(rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill&5287\\ P=\textit{initial amount}\dotfill &P\\ r=rate\to r\%\to (r)/(100)\\ t=\textit{elapsed time}\dotfill &10\\ \end{cases} \\\\\\ A=5287e^(10r) \\\\[-0.35em] ~\dotfill`

`\bf \textit{Amount of Population Growth, \boxed{\textit{21st day}}} \\\\ A=Pe^(rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill&692\\ P=\textit{initial amount}\dotfill &P\\ r=rate\to r\%\to (r)/(100)\\ t=\textit{elapsed time}\dotfill &21\\ \end{cases} \\\\\\ 692=Pe^(21r) \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \begin{cases} 5287=Pe^(10r)\\ 692=Pe^(21r) \end{cases}`

`\bf \cfrac{5287}{e^(10r)}=P\qquad therefore\qquad \stackrel{\textit{doing some substitution}}{692=Pe^(21r)\implies 692=\left( \cfrac{5287}{e^(10r)} \right) e^(21r)} \\\\\\ \cfrac{692}{5287}=\cfrac{e^(21r)}{e^(10r)}\implies \cfrac{692}{5287}=e^(21r)e^(-10r)\implies \cfrac{692}{5287}=e^(11r)`

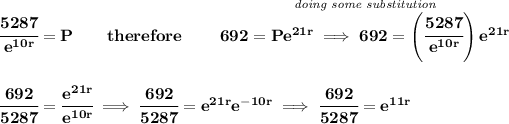
`\bf ln\left( \cfrac{692}{5287}\right)=ln\left( e^(11r) \right)\implies ln\left( \cfrac{692}{5287}\right)=11r\implies \cfrac{ln\left( (692)/(5287)\right)}{11}=r \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ ~\hfill -0.18486\approx r~\hfill`

B)

`\bf 5287=Pe^(10r)\implies 5287=Pe^(10(-0.18486))\implies 5287=Pe^(-18.486) \\\\\\ \cfrac{5287}{e^(-18.486)}=P\implies 6360.53\approx P`

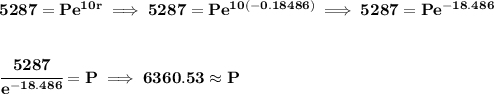
and we can round that up to a whole leaf of 6361, or truncate it to 6360, chances are is the latter.

C)

`\bf \stackrel{\textit{only 1 leaf}}{1}=(6360.53)e^(-0.18486t)\implies \cfrac{1}{6360.53}=e^(-0.18486t)\ \\\\\\ ln\left( \cfrac{1}{6360.53} \right)=ln\left( e^(-0.18486t) \right)\implies ln\left( \cfrac{1}{6360.53} \right)=-0.18486t \\\\\\ \cfrac{ln\left( (1)/(6360.53) \right)}{-0.18486}=t\implies 47.38\approx t`

and we can round that up to 47 days even.