Answer:
Option B -

Explanation:
Given : The graph attached.
To find : This graph shows the solution to which inequality ?
Solution :
The graph is passing through points (-3,-3) and (3,-1).
Applying two point slope form to get the equation of line,
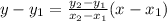
Here,
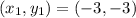 and
and
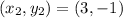
Substitute in the formula,
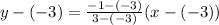
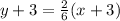
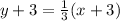
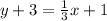
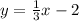
Now we see that the line approach towards origin and above the line so inequality sign is greater.
As line is dotted line so it is not equality.
The required inequality is

Therefore, option B is correct.