Question

Help solving this derivatives problem please?

Answer 1

-2^80·sin(2x)

Explanation:

First of all, the problem can be simplified a bit by recognizing the symmetry of the sine function:

sin(-2x) = -sin(2x)

Then, you need to recognize the "periodic" nature of the derivatives of the sine function:

`(d)/(dx)(-sin((2x)))=-2cos((2x))\\\\(d^2)/(dx^2)(-sin((2x)))=2^2sin((2x))\\\\(d^3)/(dx^3)(-sin((2x)))=2^3cos((2x))\\\\(d^4)/(dx^4)(-sin((2x)))=-2^4sin((2x))`

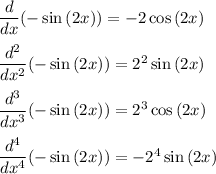
That is, the coefficient of x gets raised to the power of the derivative number, and the function (sin, cos) cycles with a repeat of 4. Thus, the 80th derivative is ...

-2^80·sin(2x)