Question

Let f(x) = -5e^(-x/3)

Find f^(6) (1)

Answer 1

Let's take the first derivative:

`f'(x) = (-5e^(-x/3))' = -5 * (e^(-x/3))' = -5e^(-x/3) * \left(-(1)/(3)\right) = (5)/(3)e^(-x/3).`

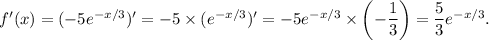
Notice that we can write this as:

`f'(x) = -(f(x))/(3).`

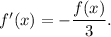
By taking the derivative of both sides
`n` times, we get:

`f^((n+1))(x) = -(f^((n)))/(3).`

This means that each time you take a derivative, a factor of
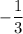`-(1)/(3)` will appear. So we conclude that:

`f^((n))(x) = \left(-(1)/(3)\right)^nf(x).`

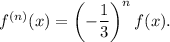
Taking
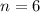`n=6` and
`x=1`, we get:

`f^((6))(1) = \left(-(1)/(3)\right)^6 f(1) = (-5e^(-1/3))/(729) = -(5)/(729)e^(-1/3).`

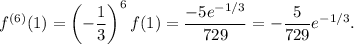
So we finally get:

`\boxed{-(5)/(729)e^(-1/3)}.`