Answer:
On the circle
Explanation:
The equation of a circle centred at the origin is
x² + y² = r² ( r is the radius )
The radius is the distance from the centre to a point on the circle.
To calculate r use the distance formula
r = √ (x₂ - x₁ )² + (y₂ - y₁ )²
with (x₁, y₁ ) = (0, 0) and (x₂, y₂ ) = (- 6,
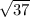 )
)
r =
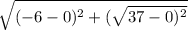
=
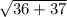 =
=

Hence
x² + y² = (
 )²
)²
x² + y² = 73 ← equation of circle
Substitute (8, 3) into the left side of the equation and
value < 73 → lies inside circle
value = 73 ← lies on the circle
value > 73 ← lies outside circle
(8, 3) → 8² + 3² = 64 + 9 = 73
(8, 3) lies on the circle