Question

What is the area of the regular polygon?

Answer 1

`(27√(3) )/(4) m^2`

Explanation:

The area of a regular polygon is given by

`Area=(1)/(2)ap`

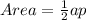
where
`a` is the apothem and
`p` is the perimeter of the triangle.

The interior angle of a regular hexagon is

`180-(360)/(6) =120\degree`

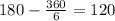
The line from the center to the given vertex bisects the 120 degree angle.

The hexagon is therefore divided into 6 equilateral triangles.

The apothem can be found using
`\sin(60\degree)=(a)/(3)`

This implies that;

`a=3\sin(60\degree)`

`a=(3√(3) )/(2)`

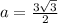
Recall that an equilateral triangle has all sides equal hence the perimeter of the regular hexagon is
`6* 3=18m^2`

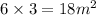
The area of the regular hexagon now becomes;

`Area=(1)/(2)* (3√(3) )/(2)* 18m^2`

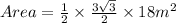
This simplifies to;

`Area= (27√(3) )/(2)m^2`