Question

EDIT// answer below thank for the help -.-

Use the parabola tool to graph the quadratic function f(x)=−x2+4.


Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.


What are the two points I need to graph? (x and y)

Answer 1

Explanation:

Move it it up 4 and then find your x intercepts.

Find the x intercepts.

`-x^2 + 4 = 0`

Move the 4 over to the right

`-x^2 = -4`

Divide out the -

`(-x^2)/(-) = (-4)/(-)`

`x^2 = 4`

Take the square root of each side

`√(x^2) = \pm √(4)`

`x = \pm \sqrt 2`

Our x intercepts are at (-2,0) (2,0)

Answer 2

A graph of the parabola with its vertex and a second point is shown on the coordinate plane in the image below.

In Mathematics and Euclidean Geometry, the vertex form of a quadratic function is represented by the following mathematical equation:

y = a(x - h)^2 + k

Where:

h and k represents the vertex of the graph.

a represents the leading coefficient.

By comparing the given quadratic function
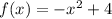`f(x)=-x^2+4` with the vertex form, we can logically deduce the coordinates of vertex;

Vertex (h, k) = (0, 4), which represents its y-intercept as well.

Next, we would determine a second point as follows;

`f(x)=-x^2+4\\\\f(1)=-(1)^2+4`

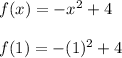
f(1) = -1 + 4

f(1) = 3.

Missing information:

Use the parabola tool to graph the quadratic function
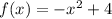`f(x)=-x^2+4`.