Answer:
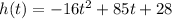 is equation of height of rocket.
is equation of height of rocket.
Option D is correct.
Explanation:
Given: A rocket is launched with speed 85 ft/s from a height 28 feet.
Launching a rocket follows the path of parabola. The equation of rocket should be parabolic.
Parabolic equation of rocket is
Formula:
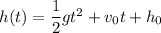
g ⇒ acceleration due to gravity (-32 ft/s)
v ⇒ Initial velocity (
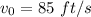 )
)
h ⇒ Initial height (
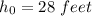 )
)
h(t) ⇒ function of height at any time t
Substitute the given values into formula
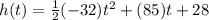
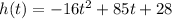
D is correct.