Answer:
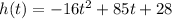 is equation of height of rocket at given time after the launch.
is equation of height of rocket at given time after the launch.
D is correct.
Explanation:
A rocket is launched at 85 ft./s from a launch pad that’s 28 feet above the ground
We have an equation of rocket launching.

Where, g is acceleration due to gravity
v is initial velocity
h is initial height
h(t) is function of height at any time t
A rocket is launched by 85 ft/s
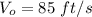
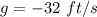

Substitute the value into formula ans get formula
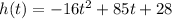
Hence, D is correct. Equation of height of rocket at given time after the launch.