Answer:
PART:A
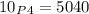
PART:B
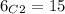
PART:C
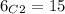
Explanation:
PART:A
When the four officers are chosen than the number of ways of doing this is:
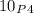
since we have to choose 4 officers and also they need to be arranged according to their ranks.
Hence, the numbers of ways doing so is:
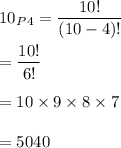
PART:B
Now we have to choose 2 members out of the remaining 6 members so the we have to use combination since we have to just choose the members and do not have to rank them or in short we can say we do not have to arrange them.
Hence, the number of ways doing this is:
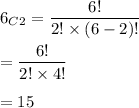
Hence, the number of ways of doing this is: 15.
PART:C
Now this process of doing so is also same as the above.
Hence, the number of ways of doing so is: 15.