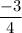Question

Use the limit theorem and the properties of limits to find the limit.
Picture below

Answer 1

We have

`(-6x^3+7x+7)/(8x^3-8x+5)=\frac{-6+\frac7{x^2}+\frac7{x^3}}{8-\frac8{x^2}+\frac5{x^3}}`

As
`x\to-\infty`, all of terms with powers of
`x` in their denominators will converge to 0, leaving you with

`\displaystyle\lim_(x\to-\infty)(-6x^3+7x+7)/(8x^3-8x+5)=\lim_(x\to-\infty)\frac{-6}8=-\frac34`

making the answer B.

Answer 2

The value of limit is
`(-3)/(4)`

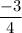
Option B is correct.

Explanation:

Given:

`L=\lim_(x\rightarrow -\infty)\left ( (-6x^3+7x+7)/(8x^3-8x+5)\right )`

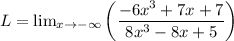
Here we have rational function whose limit is minus infinity.

Divide numerator and denominator by highest degree of polynomial (x³)

`L=\lim_(x\rightarrow -\infty)\left ( (-6+7/x^2+7/x^3)/(8-8/x^2+5/x^3)\right )`

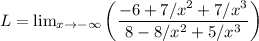
Apply limit and we get

`L=\left ( (-6+(7)/(\infty)+(7)/(-\infty))/(8-(8)/(\infty)+(5)/(-\infty))\right )`

`L=\left ( (-6+0+0)/(8-0+0)\right )`

`L=(-6)/(8)\Rightarrow -(3)/(4)`

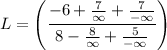
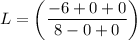
Hence, The value of limit is
`(-3)/(4)`