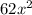Question

a family is building a rectangular fountain in the backyard. the yard is rectangular and measures 8x by 9x. The fountain is going to measure 2x by 5x. Once the fountain is built, what will be the area of the remaining yard?

Answer 1

Teachers often all this problem a donut problem because it’s like the donut hole getting cut out of the middle. The way that you solve this is to find the area of the whole yard and subtract the area of the fountain. Since they are rectangles we’re going to use A = LW
Area of yard - Area of fountain
A = (8x)(9x) - (2x)(5x)
A = 72 x^2. - 10 x^2
A 62 x^2

Answer 2

Area of rectangle(A) is given by:

`A = lw`

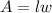
where,

l is the length and w is the width of the rectangle

As per the statement:

a family is building a rectangular fountain in the backyard. the yard is rectangular and measures 8x by 9x

⇒
`\text{Area of yard} = 8x \cdot 9x = 72x^2`

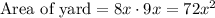
It is also given that:

The fountain is going to measure 2x by 5x.

`\text{Area of fountain} = 2x \cdot 5x = 10x^2`

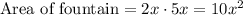
We have to find the area of the remaining yard.

`\text{Remaining area of yard} = \text{Area of yard} -\text{Area of the fountain built}`

⇒
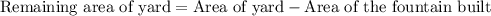
`\text{Remaining area of yard} = 72x^2-10x^2 = 62x^2` [Combine like term]

Therefore, the area of the remaining yard is,
`62x^2`