Answer:
B is correct
The value of limit is 5
Explanation:
We are given a limit
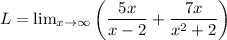
Here we need to find value of limit using limit property.
First we distribute limit
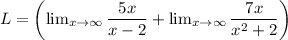
Divide each limit by x at numerator and denominator
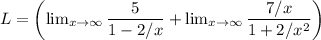
Apply limit
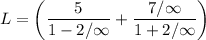
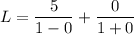
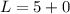
L=5
Hence, The value of limit is 5