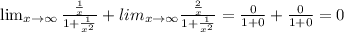Answer:
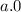
Explanation:
The given limit is
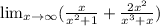
The limit of a sum is the sum of the limit
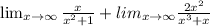
We divide the numerator and the denominator of each limit by the highest power of x in the denominator.
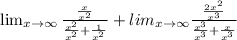
This gives us;
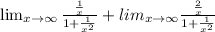
Apply the following property of limit;
As
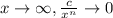 , where c is a constant.
, where c is a constant.
This will give us;