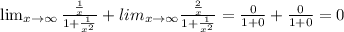Question

Use the limit theorem and the properties of limits to find the limit.

Answer 1

`a. 0`

Explanation:

The given limit is

`\lim_(x \to \infty) ((x)/(x^2+1)+(2x^2)/(x^3+x))`

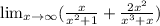
The limit of a sum is the sum of the limit

`\lim_(x \to \infty) (x)/(x^2+1)+lim_(x \to \infty) (2x^2)/(x^3+x)`

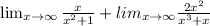
We divide the numerator and the denominator of each limit by the highest power of x in the denominator.

`\lim_(x \to \infty) ((x)/(x^2))/((x^2)/(x^2)+(1)/(x^2))+lim_(x \to \infty) ((2x^2)/(x^3))/((x^3)/(x^3)+(x)/(x^3))`

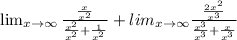
This gives us;

`\lim_(x \to \infty) ((1)/(x))/(1+(1)/(x^2))+lim_(x \to \infty) ((2)/(x))/(1+(1)/(x^2))`

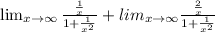
Apply the following property of limit;

As
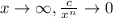`x \to \infty, (c)/(x^n) \to 0`, where c is a constant.

This will give us;

`\lim_(x \to \infty) ((1)/(x))/(1+(1)/(x^2))+lim_(x \to \infty) ((2)/(x))/(1+(1)/(x^2))=(0)/(1+0)+(0)/(1+0)=0`

Answer 2

A

Explanation:

First, simplify the expression

`(x)/(x^2+1)+(2x^2)/(x^3+x)=(x)/(x^2+1)+(2x^2)/(x(x^2+1))=(x^2+2x^2)/(x(x^2+1))=(3x^2)/(x(x^2+1)).`

Then the limit is

`\lim_(x \to \infty) (3x^2)/(x(x^2+1)).`

Since the denominator of this fraction has greater power (the power of the denominator is 3) than numerator has (the power of numerator is 2), by the limit theorem this limit is equal to 0.