Answer:
Option C.
Explanation:
The function is discontinuous at points where the denominator is equal to zero. Then we must take the polynomial that is in the denominator of the expression and look for what points is equal to zero.
Then we have the following expression:

We must factor it.
Then we look for 2 numbers that multiplied give as a result 45, and added as a result -14.
You can verify that these numbers are -9 and -5.
Then the polynomial is like:
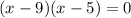
Then
 when
when
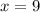 and when
and when
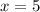
Therefore the function is continuous in all reals number except for
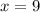 and in
and in
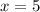
The correct option is:
Option c