Question

Explain why f(x) = √x2+4x+3/x2-x-2 is not continuous at x = -1.

Answer 1

Option C. f(x) is not defined at x = -1

Explanation:

Since given function is
`f(x) = (x^(2)+4x+3 )/(x^(2) -x-2)`

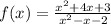
We have to check the continuity of the given function at x = -1.

We rewrite the function in the form an equation

`y = (x^(2)+4x+3 )/(x^(2) -x-2)`

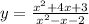
Now we factorize the fraction of the expression

`y=(x^(2)+4x+3)/(x^(2)-x-2)`

`=(x^(2)+3x+x+3)/(x^(2)-2x+x-2)`

`=((x+1)(x+3))/((x-2)(x+1))`

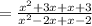
Now we can explain that for the value of x from the denominator

(x -2) = 0 Or x = 2

and for (x +1) =0

Or x = -1

The function is not continuous.

Therefore Option C is the correct answer.

Answer 2

Answer: Option C

Explanation:

Make the denominator equal to zero and solve for x:

`x^(2)-x-2=0\\(x-2)(x+1)=0\\x=2\\x=-1`

Then, as you can see, x=-1 makes the denominator equal to zero and the division by zero does not exist Therefore you can conclude that the function shown in the problem is not defined at x=-1

The answer is the option C.