Question

Can anyone solve this this problem in order please

Answer 1

Instead of using letters from A to AA, let's use numbers. Also, let's number the rows from 0 to 26. So, our labelling will go like this:

`\begin{tabular}c\text{\textbf{Row}}&\text{\textbf{Index}}\\A&0\\B&1\\C&2\\D&3\\\vdots&\vdots\\AA & 26\end{tabular}`

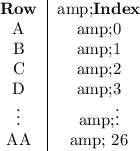
The reason for this labelling is the following: we know that row A has 9 seats, and the following rows have three more seats than the previous one. Let's build a table like the previous one, containing the number of seats for the first few rows:

`\begin{tabular}c\text{\textbf{Index}}&\text{\textbf{\# of seats}}\\0&9\\1&12\\2&15\\3&18\\4 & 21\\\vdots&\vdots\end{tabular}`

So, as you can see, the
`i`-th row has exactly
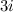`3i` more seats than the first one.

So, we have the following sequence:

`a_0=9,\ a_1=12,\ a_2=15,\ldots,\ a_n = 3n+9`

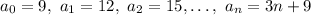
Which defines the number of seats for each row.

Answering the questions is now easy: the 27 row, AA, is the 26th term in our sequence:

`a_(26) = 3\cdot 26+9 = 78+9 = 87`

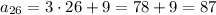
The total number of seats is the sum of all the terms in the sequence:

`\displaystyle \sum_(i=0)^(26)3n+9 = \sum_(i=0)^(26)3n + \sum_(i=0)^(26)9 = 3\sum_(i=0)^(26)n + 27\cdot 9 = 3(26\cdot 27)/(2) + 243 = 3\cdot 13 \cdot 27 + 243 = 1053 + 243 = 1296`

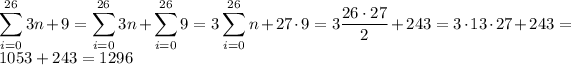
Finally, let
`a` be the number of adult tickets, and
`s` be the number of student tickets. We know that twice as many student tickets were sold as adult tickets, so we have

`s = 2a`

Since the show was a sold out, we have

`a+s = 1296 \iff a+2a = 1296 \iff 3a = 1296 \iff a = 432`

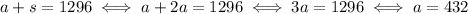
So, 432 adult tickets were sold, which implies that

`s = 432\cdot 2 = 864`

student tickets were sold. Let
`c` be the cost of a student ticket. Adult tickets then cost
`3c`, and the total revenue is

`432\cdot 3c + 864c = 1296c+864c = 2160c`

So, we have

`2160c =6480 \iff c = (6480)/(2160) = 3`