2 Answers

Priyantha · Answer 1 · 2020-11-01T22:48:12+0000

Answer:

The range is (-2,2)

The range of sinx is 1<inx<1 or −1<y<1

It implies,

−2<2sinx<2

This means that the range of y=2sinx is −2<y<2

The lower bound of the range for sine is found by substituting the negative magnitude of the coefficient into the equation.

y=−2

The upper bound of the range for sine is found by substituting the positive magnitude of the coefficient into the equation.

y =2 The range is −2≤y≤2.

ShinuShajahan · Answer 2 · 2020-11-06T00:44:33+0000

The answer is: [-2,2]

The range of a function shows where the function can exist in the y-axis.

To know the range of the function, we have to isolate x,

So

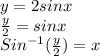
$y=2sinx\\(y)/(2)=sinx\\ Sin^(-1)((y)/(2)) = x$

The only possible values that y can take go from -2 to 2. Taking values out of these values will give as result a non-real number.

Therefore,

The range of the function is [-2,2]

Have a nice day!