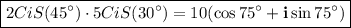Question

What is the product of 2(cos(45°) + i sin(45°)) and 5(cos(30°) + i sin(30°))?
Pls help

Answer 1

`10(\cos 75^\circ+\mathbf{i}\sin 75^\circ)`

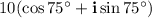
Explanation:

Complex Numbers

Complex numbers can be expressed in several forms. One of them is the rectangular form(x,y):

`Z = x+\mathbf{i}y`

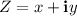
Where

`\mathbf{i}=√(-1)`

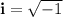
They can also be expressed in polar form (r,θ):

`Z=r(\cos\theta+\mathbf{i}\sin\theta)`

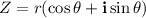
The polar form is also shortened to:

`Z = r CiS(\theta)`

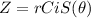
The product of two complex numbers in polar form is:

`[r_1Cis(\theta_1)]\cdot [r_2Cis(\theta_2)]=r_1\cdot r_2Cis(\theta_1+\theta_2)`

We are given the complex numbers:

2(cos(45°) + i sin(45°)) and 5(cos(30°) + i sin(30°))

They can be written as:

2CiS(45°) and 5CiS(30°). The product is:

2CiS(45°) * 5CiS(30°) = 10CiS(75°)

Expressing back in rectangular form:

`\boxed{2CiS(45^\circ) \cdot 5CiS(30^\circ) =10(\cos 75^\circ+\mathbf{i}\sin 75^\circ)}`