Question

The side-by-side boxplots show the ages of all Oscar winners for Best Actress (females) and Best Actor (males). It's easy to see that both distributions contain outliers (they're stars in the plot). Given that the median age of a man who won Best Actor is 42, Q1 = 39, and Q3 = 48, what's the maximum age of a male who would not be considered an outlier? (Use the IQR rule for outliers.)

A. 61.5

B. 75

C. 50

D. 57

Answer 1

The answer is A. 61.5

Answer 2

Answer: A. 61.5

Explanation:

According to the IQR (Interquartile range) rule , the upper fence for the dta values is given by :_

`\text{Third Quartile}+1.5* \text{IQR}`

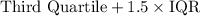
Given : First Quartile :
`Q_1=39`

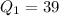
Third Quartile :
`Q_3=48`

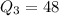
Interquartile range (IQR)=
`Q_3-Q_1=48-39=9`

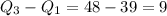
Then, Upper fence:
`48+1.5*(9)`

`=48+13.5=61.5`

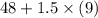
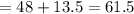
Hence, the maximum age of a male who would not be considered an outlier = 61.5