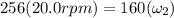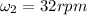Question

Two children are riding on the edge of a merry-go-round that has a mass of 100.kg and radius of 1.60m and is rotating at 20.0rpm (disc). Ignore friction. The children have masses of 22.0kg and 28.0kg and are seated on the outside (simple pendulum). If both children move to half the radius (0.8m) what is the new rotational speed?

Answer 1

Here since both children and merry go round is our system and there is no torque acting on this system

So we will use angular momentum conservation in this

`I_1\omega_1 = I_2\omega_2`

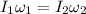
now here we have

`I_1 = (MR^2)/(2) + m_1R^2 + m_2R^2`

`I_1 = (100(1.60)^2)/(2) + (22 + 28)(1.60)^2`

`I_1 = 256`

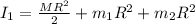
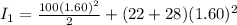
Now when children come to the position of half radius

then we will have

`I_2 = (MR^2)/(2) + m_1((R)/(2))^2 + m_2((R)/(2))^2`

`I_2 = (100(1.6)^2)/(2) + (28 + 22)(0.8)^2`

`I_2 = 160`

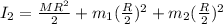
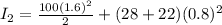
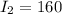
now from above equation we have

`256 (20.0 rpm) = 160(\omega_2)`

`\omega_2 = 32 rpm`