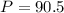Question

What is the maximum value of the objective function, P, with the given constraints?

P=3.75x+4.25y


2x+3y≤60

2x+y≤28

4x+y≤48

x≥0

y≥0




Enter your answer in the box.


P =

Answer 1

The maximum value of the objective function is
`P=90.5`

Explanation:

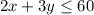`2x+3y\leq 60` -----> constraint A

`2x+y\leq 28` -----> constraint B

`4x+y\leq 48` -----> constraint C

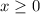`x\geq 0` ------> constraint D

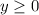`y\geq 0` ------> constraint E

using a graphing tool

The solution of the constraints is the shaded area

see the attached figure

The vertices of the shaded area are

`A(0,0),B(0,20),C(6,16),D(12,0)`

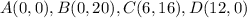
Substitute the value of x and the value of y of each vertices in the objective function to determine the maximum value

we have

`P=3.75x+4.25y`

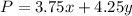
so

1) For point
`A(0,0)`

`P=3.75(0)+4.25(0)=0`

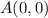
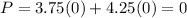
2) For point
`B(0,20)`

`P=3.75(0)+4.25(20)=85`

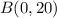
3) For point
`C(6,16)`

`P=3.75(6)+4.25(16)=90.5`

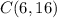
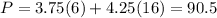
4) For point
`D(12,0)`

`P=3.75(12)+4.25(0)=45`

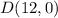
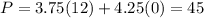
therefore

The maximum value of the objective function is
`P=90.5`