Question

Determine whether quadrilateral ABCD with vertices A(–4, –5), B(–3, 0), C(0, 2), and D(5, 1) is a trapezoid.

Step 1: Find the slope of AB. The slope of AB is .



Step 2: Find the slope of DC. The slope of DC is .



Step 3: Find the slope of BC. The slope of BC is .



Step 4: Find the slope of AD. The slope AD is .



The quadrilateral is a trapezoid because .

Answer 1

Explanation:

Answer 2

We are given a quadrilateral ABCD with vertices A(–4, –5), B(–3, 0), C(0, 2), and D(5, 1).

Step 1:

We find the slope of side AB.

with vertices A(-4,-5) and B(-3,0)

Hence, the slope of two points (a,b) and (c,d) is calculates as:

`(d-b)/(c-a)`

So, the slope of AB is:

`(0-(-5))/(-3-(-4))\\\\=(5)/(-3+4)\\\\=(5)/(1)=5`

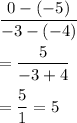
Hence slope AB=5.

Step 2:

Now we have to find the slope of DC.

with vertices D(5,1) and C(0,2)

So, the slope of DC is:

`(2-1)/(0-5)\\\\=(1)/(-5)=-(1)/(5)`

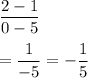
Hence slope AB=-1/5.

Step 3:

slope of BC with vertices B(-3,0) and C(0,2) is:

`(2-0)/(0-(-3))\\\\=(2)/(3)`

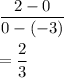
Step 4:

slope of AD with vertices A(-4,-5) and D(5,1) is:

`=(1-(-5))/(5-(-4))\\\\=(1+5)/(5+4)\\\\=(6)/(9)\\\\=(2)/(3)`

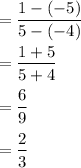
As we know that parallel sides have same slope.

As slope of BC=AD.

Hence AD is parallel to BC.

and the slope of two opposite sides are not equal hence the two sides are not parallel.

Hence, the given quadrilateral ABCD is a trapezoid. ( since it has a pair of opposite sides which are parallel and a pair of non-parallel opposite sides)