Question

if the height of the cylinder with a radius of 12 cm and a height of 20 cm has the same volume as a cone with a radius of 8 cm. what is the height of the cone​

Answer 1

`\large\boxed{H=135\ cm}`

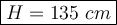
Explanation:

The formula of a volume of a cylinder:

`V=\pi r^2H`

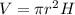
r - radius

H - height

We have the radius r = 12cm and the height H = 20cm. Substitute:

`V=\pi(12^2)(20)=\pi(144)(20)=2880\pi\ cm^3`

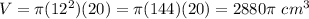
The formula of a volume of a cone:

`V=(1)/(3)\pi r^2H`

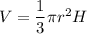
r - radius

H - height

We have the radius r = 8cm and the volume V = 2880πcm³. Substitute:

`(1)/(3)\pi(8^2)H=2880\pi\qquad\text{divide both sides by}\ \pi\\\\(1)/(3)(64)H=2880\qquad\text{multiply both sides by 3}\\\\64H=8640\qquad\text{divide both sides by 64}\\\\H=135\ cm`